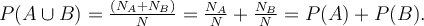Výklad - pojem pravděpodobnost
klasická, geometrická a axiomatická definice
1. Klasická definice pravděpodobnosti
Účelem počtu pravděpodobnosti je zkoumání skutečného světa pomocí matematického modelu. Takovému modelu se říká pravděpodobnostní model nebo stochastický model. Někdy je vhodné zavést ještě pomocný model, na kterém se dá matematický model snadno vysvětlit. Tento přístup je používán i v jiných oborech, ale i tam musí být konečným měřítkem porovnání výsledků matematického modelu s reálným světem.
Takovým jednoduchým modelem mohou být hrací kostky nebo mince. To neznamená, že s nimi skutečně hrajeme. Pomocí modelu si pouze některé situace snadněji představíme a svůj přístup si snadno ověříme. Sama hra v kostky nás málo zajímá.
Jinak tomu ale bylo v počátcích vývoje počtu pravděpodobnosti. Ten skutečně vznikl původně při studiu hazardních her, neboť bylo velikou záhadou, jak vlastně fungují, a proč někdo vyhraje, zatímco jiný prohraje. To ale bylo před třemi sty lety. Dnes je počet pravděpodobnosti a statistika důležitou součástí mnoha oborů.
Definice
Výsledkem pokusu může být jeden z N stejně možných výsledků. Jestliže z těchto N možných výsledků NA výsledků znamená jev A, pak pravděpodobnost jevu A definujeme jako P(A) = NA / N.
Toto vypadá jako definice kruhem, protože stejně možný znamená stejně pravděpodobný. To je obecně zakázáno, takže v tomto případě je nutné dát nějaké vysvětlení. Nejprve probereme pomocný model, například hrací kostku. Ta má šest stran, hrany a vrcholy. Vylučujeme možnost, že po hodu kostka zůstane stát na hraně nebo na vrcholu. Pokud se jedná o strany, výraz stejně možné strany můžeme interpretovat tak, že si představujeme kostku jako dokonalou krychli (dokonale symetrickou), takže nepředpokládáme, že by některá strana padala častěji než jiná. V případě matematického modelu se jedná o myšlenkový experiment. Je to předpoklad, že výsledky jsou stejně možné, čili stejně pravděpodobné. Když prohlásíme, že pravděpodobnost každého výsledku experimentu je stejná, potom jistě náš předpoklad je ekvivalentní tvrzení, že každý výsledek má pravděpodobnost 1/N, takže jejich součet musí dát jedničku. (Takový předpoklad má smysl, protože se stanoví jako hypotéza, na jejímž základě se vybuduje nějaká teorie a výsledky takové teorie se pak porovnávají s daty. Ptáme se pak, zda taková hypotéza platí nebo ne.)
Pro výpočet pravděpodobnosti jevu A potřebujeme znát, jak v čitateli počet výsledků experimentu, které mají za následek jev A, tak ve jmenovateli počet všech možných výsledků. Pro ilustraci vypočítáme pravděpodobnost toho, že při hodu jednou hrací kostkou padne jednička, což označíme jako jev A. Předpokládáme, že kostka je ideálně symetrická, takže všech šest výsledků je stejně možných. Tento počet se zapíše do jmenovatele. Pravděpodobnost jevu A je tedy P(A) = 1/6. To odpovídá tomu, že jsme si řekli, že výsledky jsou stejně možné. I zbývajících pět výsledků by dle definice mělo pravděpodobnost 1/6. To je jistě totéž jako říci, že jsou stejně možné.
Nyní za stejných předpokladů vypočteme, jaká bude pravděpodobnost, že padne sudé číslo, což označíme jako jev B. Do jmenovatele zapíšeme šestku a do čitatele počet výsledků, při kterých padne sudé číslo. Sudá čísla, která připadají v úvahu, jsou 2, 4, 6, jejich počet je tři, takže P(B) = 3/6 = 1/2.
Předpokládejme opět, že hovoříme o N stejně možných výsledcích pokusů. Tyto výsledky se nazývají elementární jevy. Mějme jev A skládající se z NA elementárních jevů. Jeho pravděpodobnost je pak definována jako počet elementárních jevů, ze kterých se skládá jev A, dělený celkovým počtem elementárních jevů.
Jev jistý S se skládá ze všech elementárních jevů. Jeho pravděpodobnost je P(S)= N/N =1. Jev nemožný se skládá z nulového počtu elementárních jevů, je to tedy prázdná množina elementárních jevů. Pravděpodobnost nemožného jevu je 0/N = 0. Předpokládejme, že se jev A skládá z NA elementárních jevů a jev B se skládá z NB elementárních jevů. Jevy A a B se nazývají NESLUČITELNÉ neboli DISJUNKTNÍ, jestliže nemají žádný společný elementární jev. Sjednocením A B jevů A a B se nazývá jev, který nastane právě tehdy, když nastane jeden nebo oba z jevů A, B. Sjednocení je možné také psát jako A nebo B a také jako A+B. Jsou-li jevy A a B disjunktní, můžeme počet elementárních jevů, ze kterých se skládá jejich sjednocení, vypočítat jako součet NA + NB, takže máme vzorec pro výpočet pravděpodobnosti sjednocení dvou disjunktních jevů
B jevů A a B se nazývá jev, který nastane právě tehdy, když nastane jeden nebo oba z jevů A, B. Sjednocení je možné také psát jako A nebo B a také jako A+B. Jsou-li jevy A a B disjunktní, můžeme počet elementárních jevů, ze kterých se skládá jejich sjednocení, vypočítat jako součet NA + NB, takže máme vzorec pro výpočet pravděpodobnosti sjednocení dvou disjunktních jevů
Tato vlastnost se nazývá ADITIVITA.
Je-li dán nějaký jev A, nazveme jeho DOPLŇKEM ten jev B, který nastane právě tehdy, když A nenastane. To je totéž, jako říci, že jev B se skládá přesně z těch elementárních jevů, které nepatří do A. Doplněk se zapíše jako S-A, kde S je množina všech elementárních jevů. Když B je doplňkem k A, je S = A  B, tudíž P(A
B, tudíž P(A  B) = P(S) = 1. Protože jsou disjunktní podle definice, platí P(A
B) = P(S) = 1. Protože jsou disjunktní podle definice, platí P(A  B)=P(A) + P(B). Je tedy 1 = P(A)+P(B) a odtud požadovaný výsledek P(B) = 1 - P(A).
B)=P(A) + P(B). Je tedy 1 = P(A)+P(B) a odtud požadovaný výsledek P(B) = 1 - P(A).