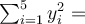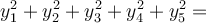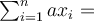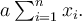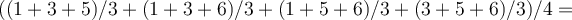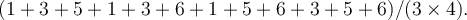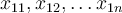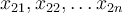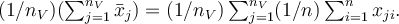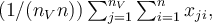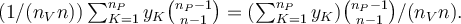Výklad - chrarakteristiky polohy dat
průměr, modus, medián, kvantily, ...
Definice a vlastnosti aritmetického průměru
O průměru jsme se učili všichni již na základní škole a od té doby mu věříme a používáme ho. Abychom ale byli schopni si jeho základní vlastnosti odvodit, nevystačíme s definicí jako sečteme a vydělíme, musíme si zavést symbol pro součet a naučit se s ním pracovat.
Když máme hovořit o 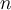 prvcích, můžeme je označit
prvcích, můžeme je označit 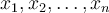 Tři tečky se čtou "až do". To znamená, že každému z čísel
Tři tečky se čtou "až do". To znamená, že každému z čísel 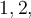 až do
až do 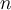 přiřadíme nějaký prvek. Těm se pak říká indexované prvky. Když jsou to čísla, tak indexovaná čísla, když jsou to proměnné, hovoříme o indexovaných proměnných. To samé někdy zapisujeme jako
přiřadíme nějaký prvek. Těm se pak říká indexované prvky. Když jsou to čísla, tak indexovaná čísla, když jsou to proměnné, hovoříme o indexovaných proměnných. To samé někdy zapisujeme jako  kde
kde  jde od
jde od  do
do 
Jednoduchým příkladem může být vyjádření, že 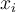 označuje čísla od jedné do sta. Zapíšeme to jako
označuje čísla od jedné do sta. Zapíšeme to jako  kde
kde  Sudá čísla od dvou do sta zapíšeme jako
Sudá čísla od dvou do sta zapíšeme jako  kde
kde 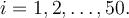
Představme si, že označíme nějaká čísla pomocí symbolů  kde
kde 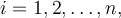 kde
kde 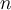 je jejich počet. Označit jejich součet je možné dvěma způsoby.
je jejich počet. Označit jejich součet je možné dvěma způsoby. 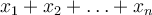 je naznačení jejich vyjmenování, ale to samé je vhodnější zapsat jako
je naznačení jejich vyjmenování, ale to samé je vhodnější zapsat jako 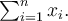 Pro symbol součtu neboli sumy se tedy používá velké řecké písmeno sigma. Celý výraz se čte suma od
Pro symbol součtu neboli sumy se tedy používá velké řecké písmeno sigma. Celý výraz se čte suma od  rovno jedné do
rovno jedné do 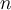 čísel
čísel 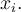 Jako příklad zapíšeme součet sudých čísel od dvou do sta jako
Jako příklad zapíšeme součet sudých čísel od dvou do sta jako 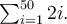 Když jsou dána čísla
Když jsou dána čísla 
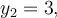

 a
a  můžeme psát
můžeme psát 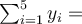

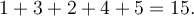 Součet s jinými mezemi je
Součet s jinými mezemi je 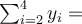
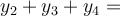
 Součet druhých mocnin je
Součet druhých mocnin je
Avšak pozor na 
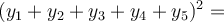

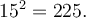 Jestliže opakovaně sčítáme nějakou konstantu
Jestliže opakovaně sčítáme nějakou konstantu  třeba
třeba 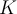 krát, zapíšeme to jako
krát, zapíšeme to jako 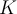 sčítanců
sčítanců 
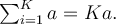 Jak je vidět, je snadné pomocí symbolu pro součet zapsat zákon komutativní, distributivní a asociativní. Například pomocí komutativního zákona pro sčítání platí
Jak je vidět, je snadné pomocí symbolu pro součet zapsat zákon komutativní, distributivní a asociativní. Například pomocí komutativního zákona pro sčítání platí 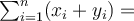
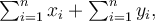 protože
protože 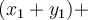
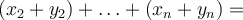
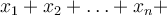
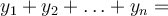
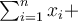
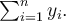
Podobně, jestliže  je konstanta, platí
je konstanta, platí
Obecnější vzorec je
Součet byl dán do závorky, protože někdy není jasné, co patří součtu a co ne.
Aritmetický průměr jako míra polohy
Když je dáno 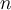 čísel
čísel  je vzorec pro průměr
je vzorec pro průměr 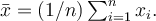 Pruhem nad symbolem pro čísla se označuje jejich průměr. Kdybychom označili nějaká čísla písmenem
Pruhem nad symbolem pro čísla se označuje jejich průměr. Kdybychom označili nějaká čísla písmenem 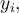 pak jejich průměr bychom značili
pak jejich průměr bychom značili 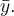 Protože při počítání průměrů je jasné, jaké meze se vyskytují v symbolu pro součet, je obvyklé je vynechávat. Zrychlí se tím psaní a zlepší se čitelnost. Když ke každé hodnotě
Protože při počítání průměrů je jasné, jaké meze se vyskytují v symbolu pro součet, je obvyklé je vynechávat. Zrychlí se tím psaní a zlepší se čitelnost. Když ke každé hodnotě 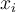 přičteme tutéž konstantu
přičteme tutéž konstantu 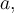 dostaneme
dostaneme 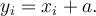 Pro průměry platí vztah
Pro průměry platí vztah 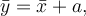 neboť
neboť 
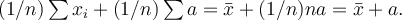 Porovnejme teploty ve stupních Celsia a v kelvinech. Právě jsme ukázali, že když
Porovnejme teploty ve stupních Celsia a v kelvinech. Právě jsme ukázali, že když 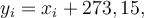 bude platit i pro průměry
bude platit i pro průměry 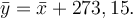 Tato základní vlastnost průměru ukazuje, že průměr je velmi vhodný jako míra polohy. Přičtením nějakého čísla k datům se totiž průměr zvýší přesně o toto číslo. Když každou hodnotu
Tato základní vlastnost průměru ukazuje, že průměr je velmi vhodný jako míra polohy. Přičtením nějakého čísla k datům se totiž průměr zvýší přesně o toto číslo. Když každou hodnotu 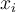 vynásobíme stejnou konstantou
vynásobíme stejnou konstantou 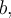 dostaneme
dostaneme 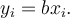 Pro průměr pak platí
Pro průměr pak platí 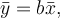 neboť
neboť 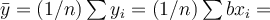
 Když udáváme délku
Když udáváme délku  v metrech a chceme ji v cm, platí
v metrech a chceme ji v cm, platí 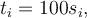 kde
kde  je délka v cm, a tudíž pro průměry platí
je délka v cm, a tudíž pro průměry platí 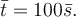 Když každou hodnotu
Když každou hodnotu 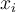 vynásobíme stejnou konstantou
vynásobíme stejnou konstantou 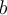 a k výsledku přičteme stejnou konstantu
a k výsledku přičteme stejnou konstantu 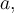 dostaneme
dostaneme 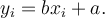 Pro průměr pak platí
Pro průměr pak platí 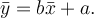 Tento vztah se snadno oveří postupným použitím vztahů předchozích nebo jako cvičení rozepsáním součtů. Jestliže
Tento vztah se snadno oveří postupným použitím vztahů předchozích nebo jako cvičení rozepsáním součtů. Jestliže 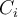 označují teplotu ve stupních Celsia a
označují teplotu ve stupních Celsia a  ve stupních Fahrenheita, je
ve stupních Fahrenheita, je 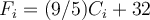 a také
a také 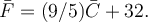
Součet odchylek od průměru.
Nejprve se budeme zajímat, jaký je součet všech odchylek od průměru. Máme-li 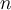 hodnot
hodnot 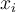 a jejich průměr
a jejich průměr  budeme jako odchylku od průměru nazývat hodnotu
budeme jako odchylku od průměru nazývat hodnotu 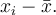 Součtem odchylek je pak
Součtem odchylek je pak  Ten lze napsat jako
Ten lze napsat jako 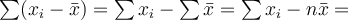
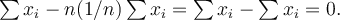 Takový výsledek říká hned několik věcí. Všechny odchylky se ruší a tudíž není možné součet odchylek použít jako míru variability. Jestliže si odchylky rozdělíme do skupin podle znaménka, to jest v první skupině budou odchylky záporné, ve druhé skupině budou odchylky kladné, případně ve třetí skupině odchylky nulové, pak součet všech odchylek kladných se všemi odchylkami zápornými dává nulu. Přesně v tomto smyslu je průměr někde uprostřed čísel, ze kterých je počítán, a rozděluje tato čísla na skupinu větší než průměr, skupinu menší než průměr a případně stejnou s průměrem. Je vhodný obrázek.
Takový výsledek říká hned několik věcí. Všechny odchylky se ruší a tudíž není možné součet odchylek použít jako míru variability. Jestliže si odchylky rozdělíme do skupin podle znaménka, to jest v první skupině budou odchylky záporné, ve druhé skupině budou odchylky kladné, případně ve třetí skupině odchylky nulové, pak součet všech odchylek kladných se všemi odchylkami zápornými dává nulu. Přesně v tomto smyslu je průměr někde uprostřed čísel, ze kterých je počítán, a rozděluje tato čísla na skupinu větší než průměr, skupinu menší než průměr a případně stejnou s průměrem. Je vhodný obrázek.
Průměr jako nevychýlený odhad (nepovinné)
Doposud jsme se zajímali o popisné vlastnosti výběru jako míry polohy. Nyní trochu odbočíme a ukážeme si vlastnost výběru, která nás opravňuje používat jej jako odhad průměru v celé populaci, když k dispozici je jen výběr. Snadno si představíme případ, kdy se populace skládá z velkého počtu prvků a nelze změřit hodnoty u všech prvků populace, abychom stanovili jejich průměr, neboli populační průměr. Statistika doporučuje, abychom provedli náhodný výběr. Z tohoto výběru pak stanovíme výběrový průměr a pomocí tohoto výběrového průměru odhadneme populační průměr. Říká se, že výběrový průměr je odhadem populačního průměru. Přesný populační průměr se nikdy nedovíme, to je pro nás jakási teoretická hodnota, kterou se snažíme odhadnout pomocí výběrového průměru, protože víme, že tento výběrový průměr bude přibližně roven populačnímu. Populační průměr přesně neznáme, máme jeho odhad. Co to ale znamená a proč si máme myslet, že výběrový průměr bude přibližně roven populačnímu? Není to jen proto, že nám nic jiného nezbývá. Chceme také vědět v jakém smyslu přibližně a co nás k tomu opravňuje. Začít se dá příkladem. Populace se skládá ze 4 prvků nabývajících hodnot 1, 3, 5, 6. Populační průměr je 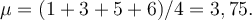 Provádíme výběry bez vracení, neboli bez opakování, aby počítání bylo co nejjednodušší a počet výběrů malý. Jako velikost výběru volíme 3.
Provádíme výběry bez vracení, neboli bez opakování, aby počítání bylo co nejjednodušší a počet výběrů malý. Jako velikost výběru volíme 3.
| výběr | výběrový průměr | ||
| 1 | 3 | 5 | (1+3+5)/3=3 |
| 1 | 3 | 6 | (1+3+6)/3=3,333 |
| 1 | 5 | 6 | (1+5+6)/3=4 |
| 3 | 5 | 6 | (3+5+6)/3=4,667 |
Ke každému výběru byl výběrový průměr zapsán do pravého sloupce, čili pro celkem čtyři výběry máme čtyři výběrové průměry. Vypočítáme nyní průměr těchto průměrů 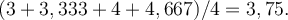 .Je důležité si všimnout, že je přesně roven populačnímu průměru. Tento jev je to, co nás opravňuje odhadovat populační průměr pomocí výběrového průměru. Jestliže se zajímáme o průměrnou velikost erytrocytu pacienta, nelze změřit všechny jeho erytrocyty. Provedeme výběr. I když ani celkový počet erytrocytů pacienta neznáme, jejich populační průměr neznáme, použijeme výběrový průměr a jím odhadneme populační průměr. Jsme k tomu oprávněni, protože průměr všech výběrových průměrů je roven populačnímu. Tato důležitá vlastnost se nazývá nevychýlenost odhadu. V následujícím se ji pokusíme ukázat pro libovolnou velikost populace i výběru. V našem příkladě průměr z průměrů je možné vypočítat jako
.Je důležité si všimnout, že je přesně roven populačnímu průměru. Tento jev je to, co nás opravňuje odhadovat populační průměr pomocí výběrového průměru. Jestliže se zajímáme o průměrnou velikost erytrocytu pacienta, nelze změřit všechny jeho erytrocyty. Provedeme výběr. I když ani celkový počet erytrocytů pacienta neznáme, jejich populační průměr neznáme, použijeme výběrový průměr a jím odhadneme populační průměr. Jsme k tomu oprávněni, protože průměr všech výběrových průměrů je roven populačnímu. Tato důležitá vlastnost se nazývá nevychýlenost odhadu. V následujícím se ji pokusíme ukázat pro libovolnou velikost populace i výběru. V našem příkladě průměr z průměrů je možné vypočítat jako
Důležité také je, že se číslo 1 opakuje třikrát a všechna další čísla také třikrát a je možné součet v závorce psát jako 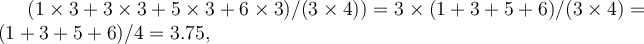 což je populační průměr, jenže počítaný z výběrů trochu jinak. Na tomto příkladě bylo ukázáno, co můžeme očekávat obecně. Bylo by naivní si myslet, že někdo bude vytvářet velká množství náhodných výběrů, aby zjistil, že tento jev funguje i pro větší výběry. U velkých populací si můžeme jen představovat všechny možné výběry. Příklad byl zvolen proto, aby byl předem naznačen přístup, který umožňuje odvodit základní vlastnost výběrového průměru.
což je populační průměr, jenže počítaný z výběrů trochu jinak. Na tomto příkladě bylo ukázáno, co můžeme očekávat obecně. Bylo by naivní si myslet, že někdo bude vytvářet velká množství náhodných výběrů, aby zjistil, že tento jev funguje i pro větší výběry. U velkých populací si můžeme jen představovat všechny možné výběry. Příklad byl zvolen proto, aby byl předem naznačen přístup, který umožňuje odvodit základní vlastnost výběrového průměru.
Nepovinná část. Pokusíme se tento jev zobecnit na libovolnou velikost populace 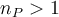 a libovolnou velikost výběru
a libovolnou velikost výběru 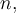 kde
kde 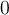 Jednotlivé prvky populace označme
Jednotlivé prvky populace označme  Při výběru bez vracení je celkový počet výběrů
Při výběru bez vracení je celkový počet výběrů 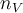 roven
roven 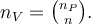 Jak je vidět na příkladě, každý prvek populace se vyskytuje ve stejném počtu výběrů. Obecně můžeme uvažovat tak, že si zvolíme libovolný prvek populace, tím v populaci zbývá jen
Jak je vidět na příkladě, každý prvek populace se vyskytuje ve stejném počtu výběrů. Obecně můžeme uvažovat tak, že si zvolíme libovolný prvek populace, tím v populaci zbývá jen  prvků a do výběru je třeba přidat jen
prvků a do výběru je třeba přidat jen 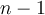 prvků. Ty vybíráme opět bez opakování a počet způsobů jakými je to možné provést je roven
prvků. Ty vybíráme opět bez opakování a počet způsobů jakými je to možné provést je roven  Označme
Označme  výběrové průměry, které jsou vypočtené z jednotlivých výběrů. Jejich počet je
výběrové průměry, které jsou vypočtené z jednotlivých výběrů. Jejich počet je 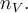 K označení hodnot z výběrů použijeme dvojité indexování,
K označení hodnot z výběrů použijeme dvojité indexování, 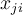 značí
značí  -tou hodnotu v
-tou hodnotu v 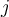 -tém výběru. Výběry je možné si představit jako
-tém výběru. Výběry je možné si představit jako
Je jich celkem 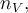 na prvním řádku je první výběr, na druhém řádku je druhý výběr a tak by to pokračovalo až do
na prvním řádku je první výběr, na druhém řádku je druhý výběr a tak by to pokračovalo až do 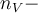 tého řádku. Ke každému řádku si představíme výběrový průměr
tého řádku. Ke každému řádku si představíme výběrový průměr 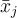 a naším úkolem je nyní výpočítat průměr ze všech těchto výběrových průměrů, což je
a naším úkolem je nyní výpočítat průměr ze všech těchto výběrových průměrů, což je
Je možné vytknout  a dostaneme vzorec
a dostaneme vzorec
Víme ale, že každá hodnota z populace se vyskytuje ve výběrech stejně krát, je tedy možné psát tento výraz jako
nyní je třeba ukázat, čemu se rovná 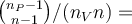
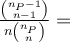
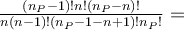
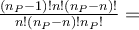
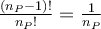 Tím je důkaz téměř proveden. Nepočítá ale s tím, že by mohla některá čísla v populaci stejná. Pak by neplatilo, že se jich nachází ve výběrech stejný počet. To se dá ale velmi snadno odstranit tak, že u každého čísla si jako index poznamenáme, z kterého měření pochází, pak je počet výběrů daný prvky obsahujících stejný a všechno pokračuje tak, jak je naznačeno. Co víme je to, že výběrové průměry dávají v průměru populační průměr. To je důležitý pojem a ve statistice se mu říká nevychýlený odhad. O přesnosti zase moc nevíme a abychom ji mohli posoudit, museli bychom znát směrodatnou odchylku výběrových průměrů pro všechny výběry. To zase nejde, protože bychom museli vytvořit všechny výběry. Je možné provést výpočet pro jednoduchý příklad jako v naše případě, ale to je zase jen ilustrace a nic víc. Na ilustračním příkladě si můžeme snadno vypočítat pravděpodobnost, že výběrový průměr je přesně roven populačnímu. Výpočet se provede tak, že se zkontroluje, že výběrový průměr není roven populačnímu ani v jednom případě, že je tedy hledaná pravděpodobnost rovna nule. Obecně může být nenulová, avšak bude velmi malá. Jenže o to tu vůbec nejde, protože s tím, že se přesně nikdy hodnotu populačního průměru nedozvíme, se musíme smířit. Jde o to, že výběrový průměr je dobrým odhadem, někdy je větší než populační průměr, někdy menší, v průměru je mu ale roven.
Tím je důkaz téměř proveden. Nepočítá ale s tím, že by mohla některá čísla v populaci stejná. Pak by neplatilo, že se jich nachází ve výběrech stejný počet. To se dá ale velmi snadno odstranit tak, že u každého čísla si jako index poznamenáme, z kterého měření pochází, pak je počet výběrů daný prvky obsahujících stejný a všechno pokračuje tak, jak je naznačeno. Co víme je to, že výběrové průměry dávají v průměru populační průměr. To je důležitý pojem a ve statistice se mu říká nevychýlený odhad. O přesnosti zase moc nevíme a abychom ji mohli posoudit, museli bychom znát směrodatnou odchylku výběrových průměrů pro všechny výběry. To zase nejde, protože bychom museli vytvořit všechny výběry. Je možné provést výpočet pro jednoduchý příklad jako v naše případě, ale to je zase jen ilustrace a nic víc. Na ilustračním příkladě si můžeme snadno vypočítat pravděpodobnost, že výběrový průměr je přesně roven populačnímu. Výpočet se provede tak, že se zkontroluje, že výběrový průměr není roven populačnímu ani v jednom případě, že je tedy hledaná pravděpodobnost rovna nule. Obecně může být nenulová, avšak bude velmi malá. Jenže o to tu vůbec nejde, protože s tím, že se přesně nikdy hodnotu populačního průměru nedozvíme, se musíme smířit. Jde o to, že výběrový průměr je dobrým odhadem, někdy je větší než populační průměr, někdy menší, v průměru je mu ale roven.