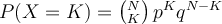Souhrn - diskrétní náhodná veličina

Diskrétní náhodné veličiny

Diskrétními náhodnými veličinami rozumíme takové náhodné veličiny, které nabývají jen konečného nebo spočetného množství hodnot.

Nejčastěji jsou studovány diskrétní náhodné veličiny, které nabývají konečného počtu hodnot, a to hodnot 0, 1, 2, …, N.

Jestliže náhodná veličina nabývá hodnot 0 až N, musí být součet všech pravděpodobností roven jedné

$\sum\limits_{i=0}^n{P(i)=1}$

Alternativní rozdělení

Jestliže náhodná veličina může nabývat jen hodnot 0 a 1 s pravděpodobnostmi q a p nazývá se takové rozdělení alternativní. Musí platit q = 1 - p.

Alternativní rozdělení reprezentuje výsledek jednoho pokusu.

Binomické rozdělení

Předpokládejme, že pravděpodobnost úspěchu v jednom experimentu je p a pravděpodobnost neúspěchu je q = 1 - p. Představme si, že provedeme nezávisle N experimentů. Při nich nám vyjde K úspěchů. Počet úspěchů K můžeme chápat jako náhodnou veličinu X, která může nabývat hodnot celočíselných od nuly maximálně do N.

$P(X=K)=\left({_K^N}\right)p^Kq^{N-K}$

Jinak řečeno, binomické rozdělení je součtem nezávislých alternativních rozdělení se stejným parametrem P, který udává pravděpodobnost úspěchu.

U binomického rozdělení záleží jen na počtu úspěchů, nikoliv na pořadí, ve kterém se úspěchy a neúspěchy vyskytnou.