Výklad - parametrické t-testy

Analýza rozptylu (angl. Analysis of Variance nebo ANOVA) je statistický test, který se používá k porovnání průměrů u několika (dvou nebo více) skupin dat. Přesněji řečeno: analýza rozptylu je prostředkem, který nám pomáhá zodpovědět otázku, zda se liší aritmetické průměry dvou nebo více populací. S pomocí analýzy rozptylu můžeme tedy například porovnat účinek několika léků na snížení hladiny cholesterolu nebo porodní hmotnost dětí matek kuřaček a nekuřaček. Jinými slovy: analýzou rozptylu můžeme například otestovat, zda snížení hladiny cholesterolu závisí na použitém léku nebo zda porodní hmotnost dětí závisí na tom, jestli je matka kuřačka. Jak je z uvedených příkladů patrné, naměřené hodnoty (hladiny cholesterolu, porodní hmotnosti) jsou realizacemi spojité náhodné veličiny, kdežto znak, který definuje porovnávané skupiny (podávaný lék, matka kuřačka/nekuřačka) je kategorický. Tomuto znaku, který určuje rozřazení do skupin, říkáme faktor. Je-li takový faktor jen jeden (jako v uvedených příkladech), mluvíme o jednofaktorové analýze rozptylu. Jestliže je faktorů více, hovoříme o vícefaktorové analýze rozptylu. Pokud například chceme ověřit, zda snížení hladiny cholesterolu závisí kromě na podaném léku také na pohlaví pacienta, musíme použít dvoufaktorovou analýzu rozptylu, neboť naměřené hodnoty cholesterolu rozřazujeme do skupin podle faktorů „lék“ a „pohlaví pacienta“.

Základní myšlenkou analýzy rozptylu je porovnání rozptylu uvnitř skupin jako míry pro variabilitu, která není ovlivněna faktorem, s rozptylem mezi skupinami, na němž by se vliv faktoru projevil.

V dalším se budeme věnovat jednofaktorové analýze rozptylu.

JEDNOFAKTOROVÁ ANALÝZA ROZPTYLU

Abychom mohli analýzu rozptylu s úspěchem použít, musí být splněny následující předpoklady:

1. všechny porovnávané výběry (i = 1,...,s) pocházejí z populací s normálním rozdělením N_i( µ_i , σ_i ² )
2. rozptyly všech těchto populací jsou shodné (tzv. homoskedasticita), tzn. σ₁² = σ₂² = ...= σ_s².

Z uvedených předpokladů vyplývá, že se srovnávané populace mohou lišit pouze průměrem. A právě na otázku, zda jsou mezi nimi alespoň dvě s rozdílným průměrem, můžeme s použitím analýzy rozptylu odpovědět.

Postup testování:

1. Jako u každého testu je nutné si nejprve stanovit NULOVOU a ALTERNATIVNÍ HYPOTÉZU a zvolit HLADINU VÝZNAMNOSTI. Jak vyplývá z předchozího, H₀: µ₁ = µ₂ = ...= µ_s a H_a: alespoň dva aritmetické průměry µ_i jsou různé. Hladinu významnosti volíme nejčastěji 5%. 

2. Dále je třeba vybrat vhodné TESTOVÉ KRITÉRIUM a vypočítat jeho hodnotu.

Základní úvahy pro konstrukci testového kritéria

Při výpočtu testového kritéria vycházíme z porovnání variability uvnitř jednotlivých skupin a mezi skupinami. Jestliže je rozptyl mezi skupinami významně větší, než rozptyl uvnitř skupin, potom se jednotlivé skupiny od sebe (v průměru) významně liší a rozdělení do skupin podle daného faktoru má smysl.

Představme si situaci, kdy hodnoty měřeného znaku neovlivňuje nic jiného než jeden faktor, a to ten, podle něhož rozřazujeme měřená data do skupin. Potom by musely být všechny hodnoty v jedné skupině stejné. Tím pádem by rozdíly mohly být jen mezi skupinami, nikoliv uvnitř skupin samotných.

Rozptyl mezi skupinami, tj. ten, který se dá vysvětlit působením faktoru, nazýváme vysvětlený rozptyl.

V praxi se ale, díky individuálním rozdílům a chybám, liší i hodnoty v rámci jedné skupiny. Tyto interindividuální odlišnosti jsou zdrojem tzv. chybového rozptylu.

Testovým kritériem je poměr vysvětleného rozptylu a rozptylu chybového.

Výpočet hodnoty testového kritéria

a) Výpočet rozptylu mezi skupinami, tj. vysvětleného rozptylu (angl. explained variance, treatment variance)

Jelikož máme k dispozici jenom výběry, můžeme provést pouze odhad vysvětleného rozptylu. Odhad provedeme tak, že všem naměřeným hodnotám v rámci jedné skupiny přiřadíme stejnou hodnotu, a to hodnotu rovnou výběrovému průměru v dané skupině. Tím „smažeme“ individuální rozdíly uvnitř jednotlivých skupin a získáme modelovou situaci, kdy jsou všechny hodnoty ve skupině stejné a rozdíly jsou pouze mezi skupinami. Z těchto „modelových“ dat vypočteme rozptyl tak, že vypočteme součet čtverců odchylek všech těchto „modelových“ hodnot od jejich průměru (tj. SC_vysvetlený) a tento součet čtverců vydělíme počtem skupin sníženým o jedničku (tj. s-1), protože nám jde pouze o rozptyl mezi skupinami a ne mezi individuálními hodnotami.

b) Výpočet rozptylu uvnitř skupin, tj. chybového rozptylu (angl. error variance)

I tento rozptyl můžeme jenom odhadnout pomocí hodnot ve výběrech. Odhad provedeme následovně. Nejprve vypočteme výběrový rozptyl v každé skupině jako odhad variability uvnitř dané skupiny. Jedním z předpokladů analýzy rozptylu je, že (populační) chybový rozptyl je uvnitř všech skupin stejný. Jako odhad tohoto rozptylu tedy vezmeme průměr výběrových rozptylů všech skupin.

c) Mezi jednotlivými složkami rozptylu existuje vztah, který se dá nazvat aditivitou součtu čtverců. Součtem čtverců se rozumí čitatel vzorce pro výpočet rozptylu.

Platí:

SC_celkový = SC_vysvetlený + SC_chybový ,

kde SC_celkový je čitatel celkového rozpylu skutečně naměřených dat a SC_chybový je součet čtverců odchylek naměřených hodnot od jejich skupinového průměru pro všechny skupiny dohromady.

Jak bylo zmíněno výše, jako testové kritérium vezmeme podíl vysvětleného a chybového rozptylu:

$F = \frac{{\frac{{SC_{vysvetleny} }}{{s - 1}}}}{{\frac{{SC_{chybovy} }}{{n - s}}}}$

Tento podíl má F-rozdělení se stupni volnosti $\nu$_vysvětlené = s – 1 a $\nu$_chybové = n – s, kde n je počet prvků ve všech výběrech dohromady.

3. VYHODNOCENÍ TESTU 

Je-li hodnota testového kritéria menší nebo rovna kritické hodnotě (získáme ji z tabulek F-rozdělení nebo v excelu funkcí FINV), nulovou hypotézu o rovnosti všech průměrů nezamítneme (protože rozptyl mezi skupinami není statisticky významně větší než rozptyl uvnitř skupin).

Je-li hodnota poměru větší než kritická hodnota, nulovou hypotézu zamítneme a přijmeme hypotézu alternativní, která říká, že mezi skupinami jsou alespoň dvě, jejichž hodnoty se v průměru významně liší. Zda se ale od sebe liší jen dvě skupiny nebo jich je více a konkrétně které skupiny se liší od kterých, analýza rozptylu neříká. Je tedy jen prvním krokem, který má rozhodnout, je-li nutné další testování. V případě, ale opravdu jen v případě, že analýzou rozptylu zamítneme hypotézu o rovnosti průměrů všech skupin, použijeme další test, např. Tukeyův post-hoc test (je nad rámec této učebnice) , který dá odpověď na otázku, které skupiny se od sebe liší.

Poznámka:

Shodu dvou populačních průměrů můžeme testovat (a také obvykle testujeme) dvouvýběrovým t-testem. Dostaneme stejný výsledek jako při použití analýzy rozptylu. Porovnáváme-li ale průměry ve více než dvou skupinách, musíme použít analýzu rozptylu. (Kdybychom místo ANOVA použili pro každou dvojici skupin dvouvýběrový t-test, nevyhnuli bychom se kumulování pravděpodobnosti chyby a, tj. pravděpodobnosti, že v některém případě zamítneme pravdivou nulovou hypotézu.)

Pro ilustraci postupu při analýze rozptylu si uveďme příklad:

Porovnáváme (na 5% hladině významnosti) vliv tří různých léků na snížení systolického krevního tlaku (STK).

Pacienty jsme rozdělili do tří skupin podle toho, který z daných léků na snížení tlaku jim byl předepsán. Z každé skupiny jsme náhodně vybrali několik pacientů. Výsledky (snížení STK v mmHg po užití jedné denní dávky léku) uvádí následující tabulka.

Předpokládejme, že všechny tři zkoumané populace mají normální rozdělení. V praxi bychom tento předpoklad měli ověřit testem normality (např. d ’ Agostinovým testem).

Postup při analýze rozptylu:

1. Definujeme nulovou a alternativní hypotézu a hladinu významnosti:

H₀: µ₁ = µ₂ = µ₃ ,

H_a: alespoň dva populační aritmetické průměry jsou různé.

α = 0,05

2. Vypočteme hodnotu testového kritéria

$F = \frac{{\frac{{SC_{vysvetleny} }}{{s - 1}}}}{{\frac{{SC_{chybovy} }}{{n - s}}}}$

Průměrné snížení v jednotlivých výběrech je následující:

Postup výpočtu SC_chybový:

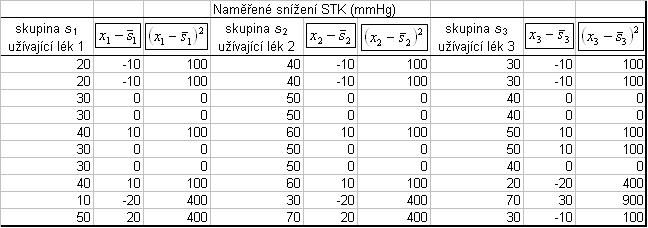
Součtem druhých mocnin všech rozdílů získáme SC_chybový.

SC_chybový = 4200.

Výpočet SC_vysvetlený:

Jak už bylo zmíněno výše, průměrné snížení v jednotlivých výběrech je

Průměrné snížení ve všech výběrech dohromady je

Všem hodnotám v prvním výběru tedy přiřadíme hodnotu 30, všem hodnotám druhého výběru 50 a hodnotám třetího výběru 40 mmHg a vypočteme rozdíly těchto hodnot od celkového průměru a poté druhé mocniny těchto rozdílů.

Součtem druhých mocnin všech rozdílů získáme SC_vysvetlený.

V našem příkladu má každý výběr 10 prvků. Můžeme tedy psát:

SC_vysvetlený = 10(30 – 40)² + 10(50 – 40)² + 10(40 – 40)² = 2000.

$F = \frac{{\frac{{2000}}{{3 - 1}}}}{{\frac{{4200}}{{30 - 3}}}}\dot = 6,4286$

V tabulkách (nebo pomocí funkce FINV v excelu) vyhledáme kritickou hodnotu F-rozdělení pro 2 a 27 stupňů volnosti. F_kritická = 3,3541.

Oborem přijetí je interval <0; 3,3541>. Hodnota testového kritéria 6,4286 je větší než kritická hodnota a spadá do oboru zamítnutí. Proto nulovou hypotézu na hladině významnosti 5% zamítneme a přijmeme hypotézu alternativní, která říká, že průměrné hodnoty se alespoň ve dvou skupinách liší.

Analýza rozptylu ukázala, že všechny tři léky nepůsobí na STK ve stejné míře. Neříká ale, zda se od sebe liší míra účinku u všech tří léků nebo jen u jedné konkrétní dvojice. K získání takovýchto informací bychom nyní museli použít ještě další test, tzv. post-hoc test. Post-hoc testů je celá řada (např. Bonferroniho test). Vycházejí často z porovnání každých dvou skupin dat pomocí t-testu, ale mají upravenou (zpřísněnou) hladinu významnosti podle počtu prováděných porovnání. Při provádění více statistických testů totiž roste pravděpodobnost, že někde vyjde statisticky významný výsledek pouze náhodou. Proto je žádoucí odpovídajícím způsobem hladinu významnosti korigovat.