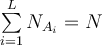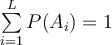Výklad - rozdělení četností
absolutní a relativní četnost
Základní vlastnosti relativních četností
S relativními četnostmi se nejdříve setkáváme ve statistice při studiu intervalových četností. Tam se jedná o popis souboru čísel, ale je vhodné se zajímat o širší souvislosti. Relativními četnostmi se můžeme zabývat i bez odkazu na intervaly, když zdůrazníme, že jsou vhodné pro popis kategorických dat. Nakonec přechod od původních hodnot k intervalům je jen přechod od kvantitativních dat ke kategorickým s k tomu patřící ztrátou informace, jak je třeba neustále zdůrazňovat.
Absolutní četnosti popisují, kolikrát se kategorie vyskytla bez vztahu k celku, zatímco relativní četnost naopak vztahuje četnost k celku. Tím se dostáváme k tomu, že nás nezajímá, kolikrát se kategorie vyskytla, ale spíš nám jde o to, jak často se kategorie vyskytla vzhledem k celkovému počtu výskytů v ostatních kategoriích.
Pro relativní četnost kategorie A použijeme označení P(A) a podle definice je P(A) = NA/N, kde NA je absolutní četnost kategorie A a N je celkový počet výskytů ve všech kategoriích.
Sjednocení C dvou kategorií A a B se označuje jako C = A U B. C nastane, když nastane A nebo B, což může znamenat jedna z nich nebo obě. Používá se i označení C = A nebo B a také C = A + B.
Kategorie je vhodné definovat tak, aby měly vhodné vlastnosti. Nejdůležitější je neslučitelnost kategorií. Dvě kategorie se nazývají neslučitelné, když nemohou nastat obě zároveň. Pro absolutní četnosti pak platí NC = NA + NB, protože buď nastane A nebo B, ale ne obě. Toto pravidlo o součtu se přenáší na relativní četnost, což se zapíše jako P(C) = P(A) + P(B). To plyne z toho, že P(C) = NC/N = (NA + NB)/N = NA/N + NB/N = P(A) + P(B). Toto je velmi důležitá vlastnost, nazývá se aditivnost.
Povšimněme si souvislosti s množinami. Ať hovoříme o populaci nebo o výběru, skládají se z nějakých prvků. Kategorie rozdělují nějak tyto prvky do množin. Jestliže tyto množiny jsou vždy disjunktní, je to totéž jako říci, že kategorie jsou neslučitelné. Je nutné zdůraznit, že musí být disjunktní vždy a že to znamená nejen pro jeden výběr, ale pro všechny možné výběry, aby se předešlo těžkostem.
Spojení dvou kategorií pak, v uvedeném smyslu, není nic jiného než sjednocení množin. Jestliže se navíc jedná o sjednocení C = A U B množin disjunktních, platí, že počet prvků ve sjednocení dvou množin je roven součtu počtů prvků v obou množinách. To není nic jiného než výrok o absolutních četnostech NC=NA+NB.
Pro ilustraci je vhodný příklad kategorie majitelů koček a kategorie majitelů psů. Nejsou neslučitelné, protože někteří lidé mají jak kočku, tak psa. Součet počtu majitelů koček a počtu majitelů psů nedá počet majitelů koček nebo psů. Nemůžeme tudíž použít pravidlo pro sčítání, protože tyto kategorie nejsou neslučitelné, což je velmi nepříjemné. Je žádoucí v takovém případě zavést další kategorii majitelů psů a koček zároveň, pak jsou kategorie disjunktní a můžeme relativní četnosti sčítat.
Dalším základním požadavkem je, aby kategorie byly vyčerpávající, to znamená, aby všechny možnosti byly zahrnuty. Tato vlastnost, pokud jsou kategorie zároveň neslučitelné, má ten závažný důsledek, že počet všech výskytů se musí rovnat součtu počtů výskytů v jednotlivých kategoriích. Z toho vidíme, že označíme-li kategorie A1, A2,…, AL a tyto kategorie jsou neslučitelné a vyčerpávající, pak pro absolutní četnosti platí:
Dělíme levou i pravou stranu N a dostaneme pro relativní četnosti:
Na příkladě se psy a kočkami vidíme, že vyjmenované kategorie nejsou vyčerpávající a že musíme použít ještě další. Můžeme přidávat majitele dalších domácích zvířat a musíme též vytvořit kategorii pro lidi, kteří nejsou majiteli žádných domácích zvířat.
Záleží samozřejmě na definici populace, abychom mohli říci, zda kategorie jsou vyčerpávající. Někdy je účelné zavést kategorii ostatních. Například uvedeme majitele psů, majitele koček, majitele psů a koček, majitele ostatních domácích zvířat a ty, kteří nevlastní žádná domácí zvířata.
K základním vlastnostem si přidáme ještě to, že absolutní a tedy i relativní četnosti jsou nezáporné a tudíž musí být větší nebo rovny nule.
Pokud se budeme řídit těmito základními pravidly, můžeme s relativními četnostmi leccos počítat, aniž bychom znali, čeho se týkají. To je jistě podstatné zobecnění. V zobecňování můžeme jít i dále. Maximálně tak daleko, že nám je jedno, jak vůbec zkoumaná čísla vznikla, stačí, když mají vlastnosti stejné jako relativní četnosti. Tím se dostáváme k počtu pravděpodobnosti.
Počet pravděpodobnosti je svou podstatou teoretickým výpočtem relativních četností. Sám o sobě by počet pravděpodobnosti byl jen teorie, ale ve vztahu k relativním četnostem dává možnosti mnoha aplikací. Teoretický model je možné vybudovat na základě spekulativních základů. Ty ale musí odpovídat skutečnosti reálného světa tak, aby byly ve shodě s pozorovanými relativními četnostmi.
Tím, že jako základní pravidla pro počet pravděpodobnosti dáváme pravidla pro počítání s relativními četnostmi a jejich vztah k teorii jako základní myšlenku, tím také naznačujeme, že počet pravděpodobnosti se zabývá jevy hromadnými. Nikoliv tedy jevy, které se nemohou opakovat. I v případě jen několika experimentů jejich opakovatelnost spočívá spíš v možnosti opakování.
Naopak, pokud se něco přihodilo jen jednou, neměl by se počet pravděpodobnosti použít. Tím bychom ale zakázali všechny aplikace například v ekonomii, takže je třeba vzít v úvahu spíš opakování stejných podmínek. Pokud to nejde, nelze výpočty použít. Známým příkladem jsou revoluce, po kterých se společenské vztahy podstatně mění a některá data a úvahy z předrevolučních období se nedají použít. Podobně bychom mohli uvažovat o stavu pacienta před nějakým podstatným zákrokem a po něm.
Příklad: V souboru 50 červených krvinek byly vypočteny následující četnosti:
| Intervaly | Absolutní | Relativní | Kumulativní | Kumulativní |
|
četnosti |
četnosti |
absolutní čet. | relativní čet. | |
| 4,0 - 4,9 | 0 | 0,00 | 0 | 0,00 |
| 5,0 - 5,9 | 1 | 0,02 | 1 | 0,02 |
| 6,0 - 6,9 | 10 | 0,2 | 11 | 0,22 |
| 7,0 - 7,9 | 16 | 0,32 | 27 | 0,54 |
| 8,0 - 8,9 | 16 | 0,32 | 43 | 0,86 |
| 9,0 - 9,9 | 7 | 0,14 | 50 | 1,00 |
| 10,0 - 10,9 | 0 | 0,00 | 50 | 1,00 |